Simonxie's Workshop

Mathematical Derivation of EWA Filtering

Computer Graphics
2025/02/19
loading

Introduction & Intuition

In texture anisotropic filtering, we have one basic problem: antialiasing. If the projection distortion is big, pixels at further area appear aliased. For example, take a look at this picture:

The underlying reason is: different screen-space pixels span different area in texture space.

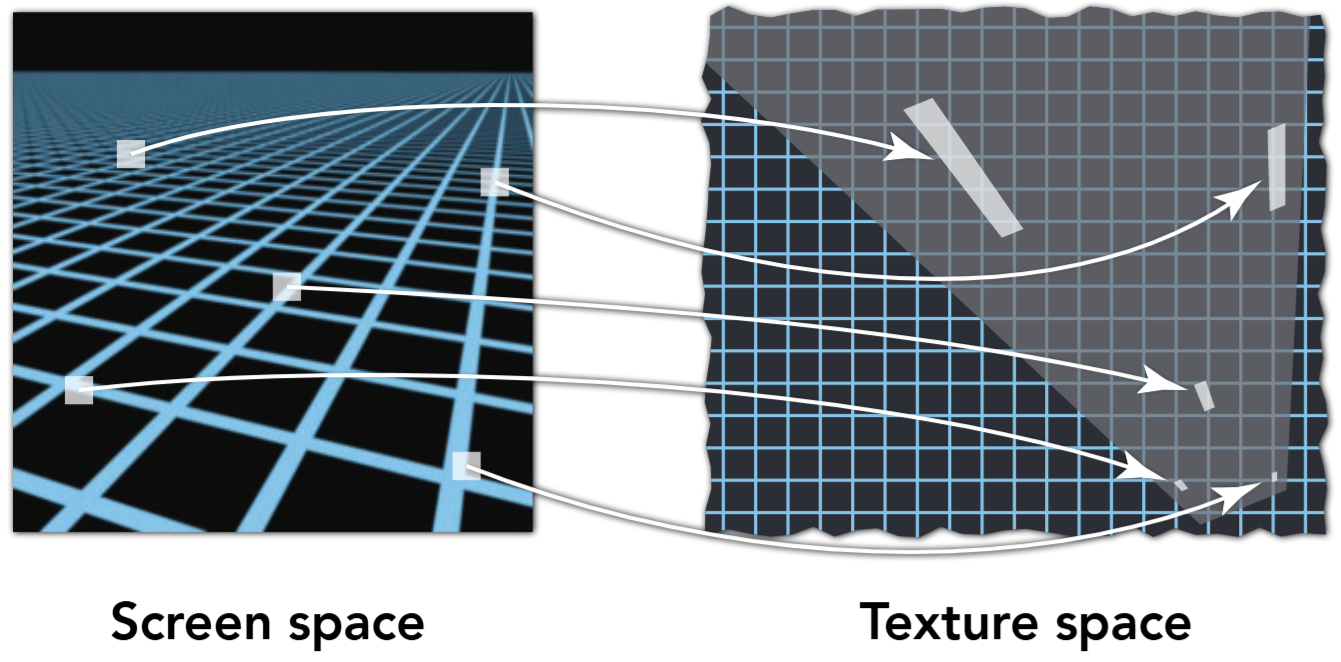
So, we want to know how a pixel in screen space is projected to texture space. This involves two main parts:

  1. If the pixel is projected to texture space, which area will it span?
  2. Given the area that a screen pixel span in texture space, how should we average their color?

This is where ewa filtering comes in.

Mathematical Induction

Projecting Pixels

First, we need to know how a screen pixel is projected to texture space. We mainly focus on unit vectors: How are \(dx\) and \(dy\) projected?

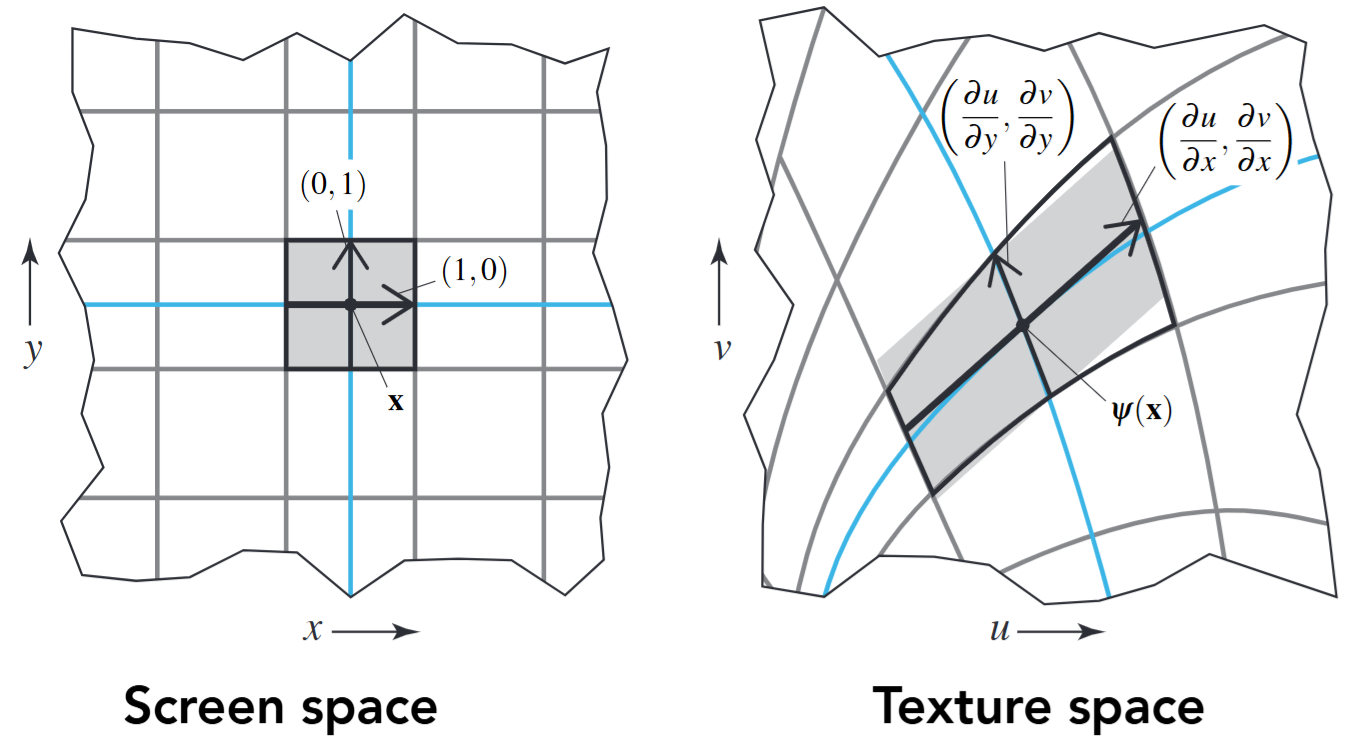
The answer is quite simple! You just need to calculate the barycentric coordinates to determine the relative position of the points to the triangle vertices. Then, you may use the barycentric coordinates to weighted average your vertex uvs. The pseudocode is:

1
2
3
4
5
6
7
8
9
10
11
12
def project_screen_point_to_uv_space(
	point: Vector2D, # a point on screen space, to be projected
    triangle_vertex_1: Vector2D, triangle_vertex_1_uv: Vector2D, 
    triangle_vertex_2: Vector2D, triangle_vertex_2_uv: Vector2D, 
    triangle_vertex_3: Vector2D, triangle_vertex_3_uv: Vector2D, 
): 
    alpha, beta, gamma = calc_barycentric_coordinate(
        point, triangle_vertex_1, triangle_vertex_2, triangle_vertex_3
    )
    return alpha * triangle_vertex_1_uv + \
		   beta  * triangle_vertex_2_uv + \
		   gamma * triangle_vertex_3_uv

As long as we can project points, we can project vectors!

This is how we calculate \((\frac{du}{dx}, \frac{dv}{dx}), (\frac{du}{dy}, \frac{dv}{dy})\).

Understanding Jacobians (As Linear Transforms)

The above process can be written in a simple mathematical formula, i.e. \[ J = \frac{\partial(u, v)}{\partial(x, y)} = \begin{bmatrix} \frac{du}{dx} & \frac{du}{dy} \\ \frac{dv}{dx} & \frac{dv}{dy} \end{bmatrix} \] What does this matrix mean? (You can first think of your answer and then go forward.)

Actually, this matrix is a linear approximation of the distortion at screen-position \((x_0, y_0)\). Mathematically speaking, for a very small area around \((x_0, y_0)\), we have the following formula exists: \[ \begin{bmatrix} \Delta u \\ \Delta v\end{bmatrix} = \begin{bmatrix} \frac{du}{dx} & \frac{du}{dy} \\ \frac{dv}{dx} & \frac{dv}{dy} \end{bmatrix} \begin{bmatrix} \Delta x \\ \Delta y\end{bmatrix}, \quad \forall \hspace{0.1cm} \|(\Delta x, \Delta y)\| < \epsilon \] where: \[ \Delta x = x - x_0, \quad \Delta y = y - y_0 \] Why is this? Lets do some matrix partition. We let vector \(\vec{uv}_i\) be the i-th column of the Jacobian matrix as follows. \[ J = \frac{\partial(u, v)}{\partial(x, y)} = \begin{bmatrix} \frac{du}{dx} & \frac{du}{dy} \\ \frac{dv}{dx} & \frac{dv}{dy} \end{bmatrix} = \begin{bmatrix} \vec{uv}_0 & \vec{uv}_1\end{bmatrix} \] This means that \(J\), as a linear transform / matrix product, can be written in this form: {suppose we DON'T know that \([\Delta u, \Delta v]^T = J \cdot [\Delta x, \Delta y]^T\) now} \[ J \cdot \begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix} = \begin{bmatrix} \vec{uv}_0 & \vec{uv}_1\end{bmatrix} \cdot \begin{bmatrix} \Delta x \\ \Delta y\end{bmatrix} = \Delta x \cdot \vec{uv}_1 + \Delta y \cdot \vec{uv}_2 \] If we view \(\vec{uv}_i\) as a set of basis vector in a new space (expressed under original space's basis), this is just a linear transform! This is no surprise, because \(\vec{uv}_i\) are exactly the projected unit vectors centered at \(x_0, y_0\) in screen space.

Projecting Screen-Space Gaussians

In the previous part, we have already solved the first problem: If the pixel is projected to texture space, which area will it span. This is nothing more than a projection (from screen space to texture space).

Now, let's derivate the second problem: given the area that a screen pixel span in texture space, how should we average their color (using different weights)? This is the core of ewa filtering: a 2d gaussian weight matrix.

To be more specific, we actually want to know such a gaussian kernel:

  1. It is originally centered at your sampling position, i.e. \(\mathcal{N}((x_0, y_0), ...)\) in screen space.
  2. It is originally a normalized distribution in screen pixel space , i.e. \(\mathcal{N}(..., 1)\)
  3. What is its distribution after projection to texture space?

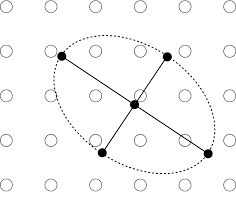
We can write its distribution formula in screen space: \[ f(x, y) = \frac{1}{2\pi} e^{-\frac{1}{2} (dx^2 + dy^2)} = \frac{1}{2\pi} e^{-\frac{1}{2} \begin{bmatrix}dx & dy\end{bmatrix} \cdot \begin{bmatrix}dx \\ dy\end{bmatrix}} \] We know that there exist such relation between \((x, y)\) and \((u, v)\): \[ \begin{bmatrix} x \\ y\end{bmatrix} = \begin{bmatrix} \frac{du}{dx} & \frac{du}{dy} \\ \frac{dv}{dx} & \frac{dv}{dy} \end{bmatrix} ^ {-1} \begin{bmatrix} u \\ v \end{bmatrix} = J^{-1} \begin{bmatrix} u \\ v \end{bmatrix} \] Hence, the distribution can be reparametrized by substitution: \[ \begin{aligned} f(x, y) &= \frac{1}{2\pi} e^{-\frac{1}{2} \begin{bmatrix}dx & dy\end{bmatrix} \cdot \begin{bmatrix}dx \\ dy\end{bmatrix}} \\ &= \frac{1}{2\pi} e^{-\frac{1}{2} \begin{bmatrix}du & dv\end{bmatrix} \cdot J^{-T} \cdot J^{-1} \cdot \begin{bmatrix}du \\ dv\end{bmatrix}} \\ &= \frac{1}{2\pi} e^{-\frac{1}{2} \begin{bmatrix}du & dv\end{bmatrix} \cdot (J J^T)^{-1} \cdot \begin{bmatrix}du \\ dv\end{bmatrix}} \\ \end{aligned} \\ \] This is the projected gaussian kernel on texture space: \[ \begin{aligned} f(u, v) &= \frac{1}{2\pi} e^{-\frac{1}{2} \begin{bmatrix}du & dv\end{bmatrix} \cdot \Sigma \cdot \begin{bmatrix}du \\ dv\end{bmatrix}} \\ \end{aligned} \\ \] where \[ \Sigma = (J J^T)^{-1} \]

Averaging Texels

Now that we already have the weight parameters in texture space, we are very happy to sample the corresponding color as \((x_0, y_0)\)'s color!

By expanding the matrix products, we have the following expression: \[ ({\frac{du}{dx}}^2 + {\frac{dv}{dx}}^2) {\Delta u}^2 + (\frac{du}{dx}\cdot \frac{du}{dy} + \frac{dv}{dx} \cdot \frac{dv}{dy})2\Delta x \Delta y + ({\frac{du}{dy}}^2+{\frac{dv}{dy}}^2){\Delta y}^2 = 0 \] Hence the parameters \(A, B, C\) of the ellipse is given as: \[ A \cdot {\Delta u}^2 + 2B \cdot \Delta x \Delta y + C \cdot {\Delta y}^2 = 0 \] where: \[ A = {\frac{du}{dx}}^2 + {\frac{dv}{dx}}^2 \\ B = \frac{du}{dx}\cdot \frac{du}{dy} + \frac{dv}{dx} \cdot \frac{dv}{dy} \\ C = {\frac{du}{dy}}^2+{\frac{dv}{dy}}^2 \] Therefore, take \((u_0, v_0)\) as the (projected) center of sampling, we can do gaussian weighted average of each pixel in an area, i.e. \[ \text{Color}(u_0, v_0) = \frac{\sum_{\Delta u, \Delta v} \text{weight}(\Delta u, \Delta v) \cdot \text{Color}(u+\Delta u, v+\Delta v)}{\sum_{\Delta u, \Delta v}\text{weight}(\Delta u, \Delta v)} \] where the weight is given as follows: \[ \text{weight}(\Delta u, \Delta v) = A\cdot {\Delta u}^2 + B \cdot \Delta u\Delta v + C \cdot \Delta v^2 \]

Question Left for Readers

Usually, we require the new basis \(\vec{uv}_i\), i.e. the columns of linear transform \(J\), to be orthogonal. Do we need to do Gram-Schmidt normalization on the vectors \(\vec{uv}_i\)?

(The answer is, No! Think about it~)

Here are my render results. Pay attention to the distant part of the ground plane and the top surface of the block. You can zoom-in by clicking on the image.

Bilinear + Bilinear + MSAA1x Bilinear + EWA + MSAA1x
Bilinear Pixel + Bilinear Level + MSAA1x Bilinear Pixel + EWA Filtering + MSAA1x

My Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
// Inside namspace CGL
Color Texture::sample_ewa(SampleParams sp, int level) {
    auto& mip = mipmap[level];

    float J00 = (sp.p_dx_uv[0] - sp.p_uv[0]) * mip.width;
    float J01 = (sp.p_dy_uv[0] - sp.p_uv[0]) * mip.width;
    float J10 = (sp.p_dx_uv[1] - sp.p_uv[1]) * mip.height;
    float J11 = (sp.p_dy_uv[1] - sp.p_uv[1]) * mip.height;

    float A = J00 * J00 + J10 * J10;
    float B = 2.0f * (J00 * J01 + J10 * J11);
    float C = J01 * J01 + J11 * J11;

    float det = sqrtf((A - C) * (A - C) + B * B);
    float lambda1 = (A + C + det) * 0.5f;
    float lambda2 = (A + C - det) * 0.5f;
    float sigma = 2.0f * sqrtf(std::max(lambda1, lambda2));
    float radius = std::min(3.0f * sigma, 15.0f);

#if DEBUG
    std::cout << std::format("l1, l2: {}, {}", lambda1, lambda2) << std::endl;
#endif

    int u_min = std::max(0, int(sp.p_uv[0] * mip.width - radius));
    int u_max = std::min((int)mip.width - 1, int(sp.p_uv[0] * mip.width + radius));
    int v_min = std::max(0, int(sp.p_uv[1] * mip.height - radius));
    int v_max = std::min((int)mip.height - 1, int(sp.p_uv[1] * mip.height + radius));

#if DEBUG
    std::cout << std::format("Sampling: {}, {}, {}, {}", u_min, v_min, u_max, v_max) << std::endl;
#endif

    Color color_sum(0, 0, 0);
    float weight_sum = 0.0f;

#if DEBUG
    std::cout << "=================" << std::endl;
#endif

    for (int u = u_min; u <= u_max; ++u) {
        for (int v = v_min; v <= v_max; ++v) {
            float du = (u + 0.5f) - sp.p_uv[0] * mip.width;
            float dv = (v + 0.5f) - sp.p_uv[1] * mip.height;

            float weight = expf(-0.5f * (A*du*du + B*du*dv + C*dv*dv));

#if DEBUG
	        std::cout << weight << " ";
#endif

            color_sum += sample_bilinear(sp.p_uv, level) * weight;
            weight_sum += weight;
        }

#if DEBUG
	std::cout << std::endl;
#endif
    }

    if (weight_sum > 0.0f) {
        color_sum *= 1 / weight_sum;
    }

    return color_sum;

    // default to magenta for invalid items
    // return Color(1, 0, 1);
}

Author：SimonXie2004

Link：https://simonxie2004.github.io/2025/02/19/EWA-Filter/

Publish date：February 19th 2025, 7:54:39 pm

Update date：April 8th 2025, 11:59:30 pm

License：CC-4.0

CATALOG
  1. 1. Introduction & Intuition
  2. 2. Mathematical Induction
    1. 2.1. Projecting Pixels
    2. 2.2. Understanding Jacobians (As Linear Transforms)
    3. 2.3. Projecting Screen-Space Gaussians
    4. 2.4. Averaging Texels
  3. 3. Question Left for Readers
  4. 4. Result Gallery
  5. 5. My Code
Total : 15
2025
2024
Artificial Intelligence Cheatsheet Computer Vision Image Processing Computer Graphics Physics Simulation GLSL Shader Deep Learning Generative Models Image Metrics Rasterization New View Synthesis Path Tracing Computer Security
UCB-AI UCB-CV-Project UCB-CV UCB-CG-Project Technical Blog UCB-Security