Face-Morphing

 2024/10/07 

UC-Berkeley 24FA CV Project 3 - Face Morphing, Human Faces Averaging, and Face-PCAs.

Face Morphing

Overview

In this assignment we will:

Produce a "morph" animation of one's face into someone else's face
Compute the mean of a population of faces
Extrapolate from a population mean to create a caricature of oneself.

A morph is a simultaneous warp of the image shape and a cross-dissolve of the image colors. The cross-dissolve is the easy part; controlling and doing the warp is the hard part. The warp is controlled by a human-defined correspondence between the two pictures. The correspondence should map eyes to eyes, mouth to mouth, chin to chin, ears to ears, etc., to get the smoothest transformations possible.

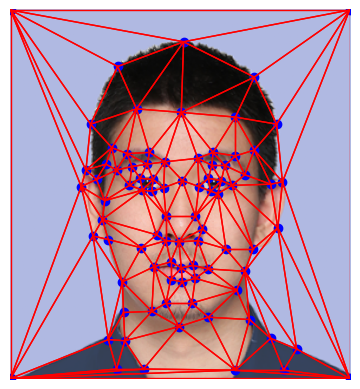
Part I: Defining Correspondences

Use this tool to define correspondences
Implement the delaunay triangulation algorithm.

*Remark: two images must have same Delaunay triangulation (because the triangles must be one-to-one correspondent for two images), hence delaunay is only called once!

Creating Delaunay Triangulation. Image cited from CS180, UC Berkeley, Alexei Efros.
Here is an example of results

Part II: Compute the Mid-Way Face

First, we define computeAffine(tri1, tri2), which calculates the affine transform between two triangles.

This is equivalent to solving this matrix transform (under homogeneous coordinate system): \[ \begin{pmatrix} a & b & tx \\ c & d & ty \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ 1 & 1 & 1 \end{pmatrix} = \begin{pmatrix} x_1' & x_2' & x_3' \\ y_1' & y_2' & y_3' \\ 1 & 1 & 1 \end{pmatrix} \]
Then, compute the mid-way face! This would involve:
1. Computing the average shape (a.k.a the average of each keypoint location in the two faces)
2. Warping both faces into that shape (a.k.a apply affine transforms separately)
  
  *Remark: This will involve rasterization of triangles (so as to determine the pixels inside different triangles, and transform them with different affine matrices.)
  
  *Remark: Suppose we have image A and C and we want to create image B. We can warp B to A and B to C separately, so we can sample the color by bilinear interpolation.
3. Averaging the colors together.
  
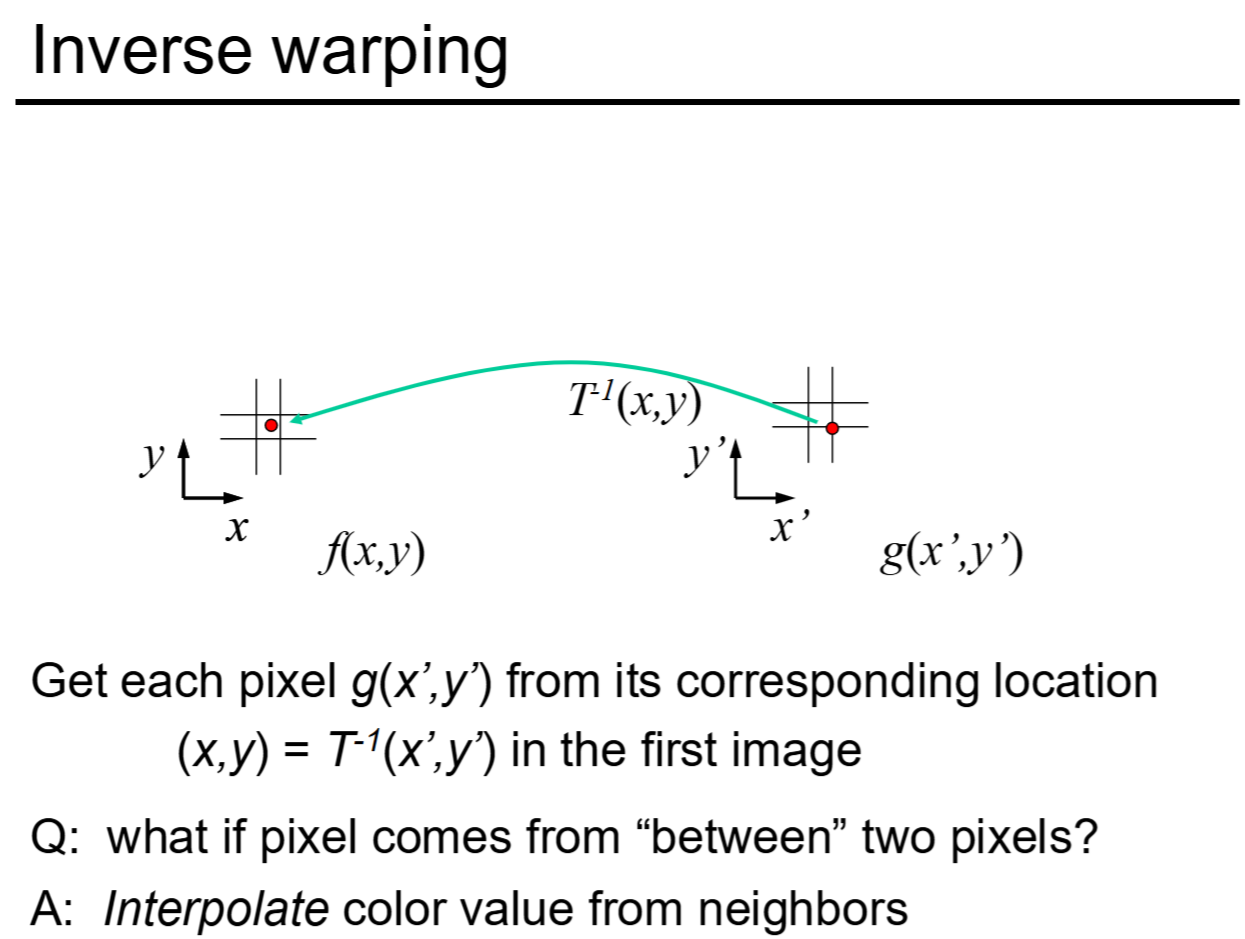
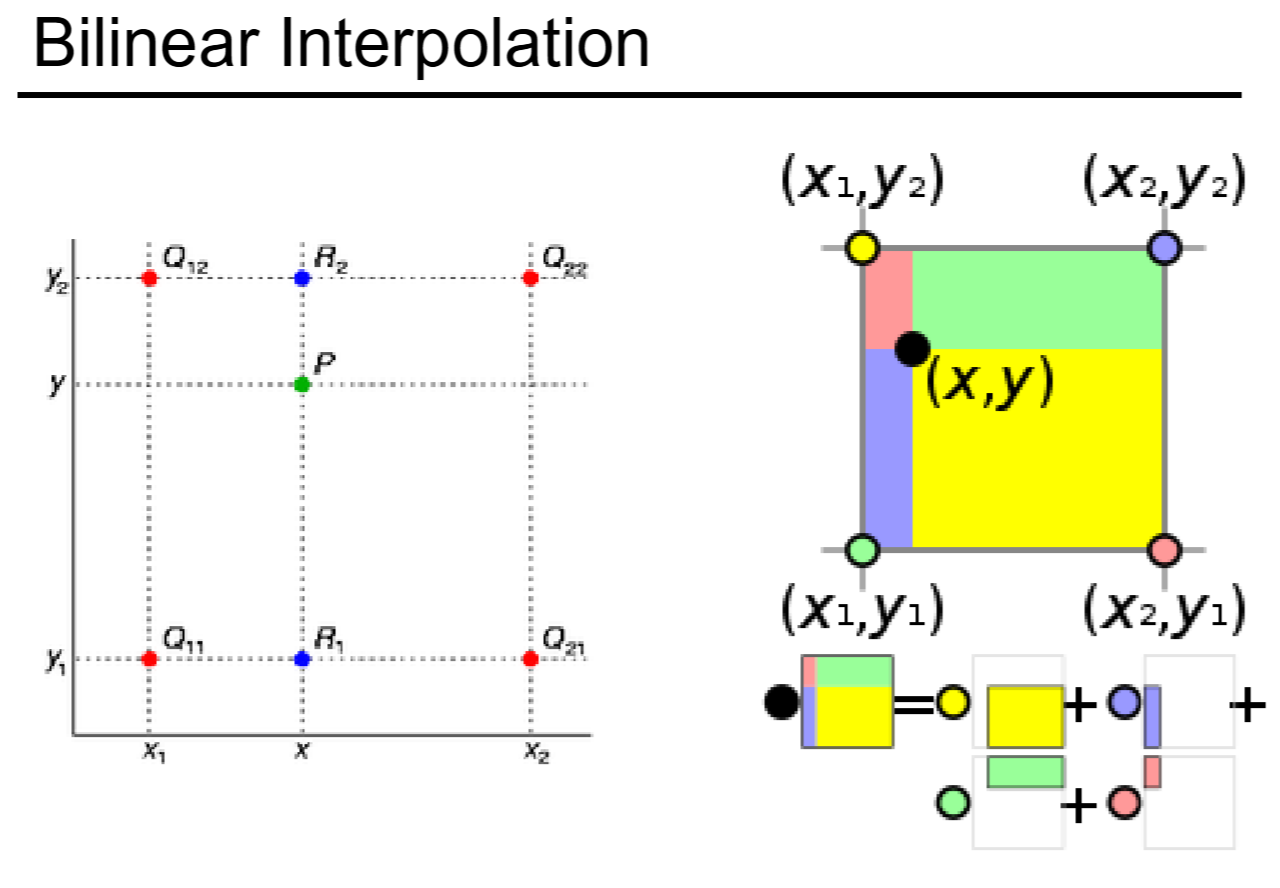
  Using inverse transform and bilinear interpolation to morph images.
  
  Image cited from CS180, UC Berkeley, Alexei Efros.
Here is an example result:

Part III: Create Morph Sequence

As long as we can morph the mid-way image, we can morph any sequence just like linear-interpolation!

The result is given by avgColor = c1*t + c2*(1-t), and we warp the image into avgPts = pts1*t + pts2*(1-t)
Here is an example result:
To make the result more fluent, we can implement a sigmoid function to make the animation non-linear.
The final result is given by:

Part IV: The "Mean face" of a population

In this part, we create a population's mean face!
Here, we choose the dataset FEI Database and IMM Database, which include some subpopulation's faces and their annotated points.
1. FEI Database is a dataset on Brazilians. It includes 100 images for male, female, male_smiling, female_smiling respectively.
2. IMM Database is a dataset on Danish. For each people, six images with either different poses or emotion are taken.
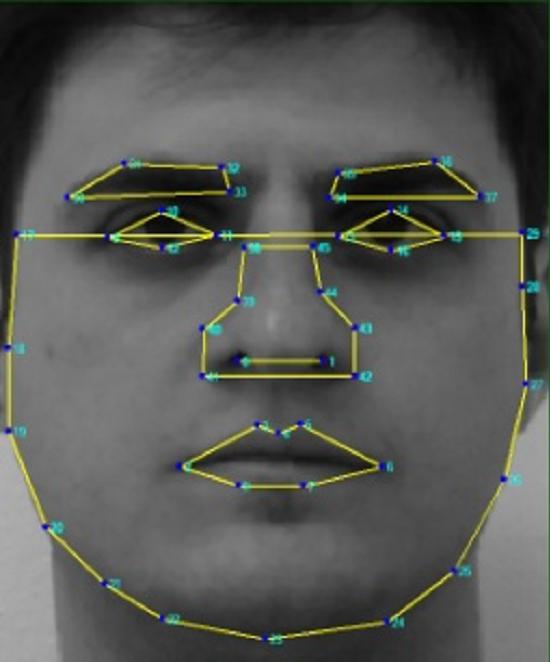
An example image visualized with annotated points from FEI dataset
We compute mean face by an approach similar to face morphing. Simply calculating mean pts, morph each face into that pts and average them will produce an awesome result!
For FEI Dataset, here is the average face for all male/female.
For IMM Dataset, here is the average face for all male/female.
Also, a few interesting experiments can be done.
1. We can morph some images in the dataset to the average face on that dataset, and see what happens.
2. We can morph a picture of me to one dataset, or morph that dataset's average face to mine.

Part V. Caricatures: Extrapolating from the mean

This part produce a caricature of my face by extrapolating from the population mean calculated in the last step.

Suppose we want to make it more "Danish" or farther from "Danish" (i.e. we are using the IMM mean face above.)
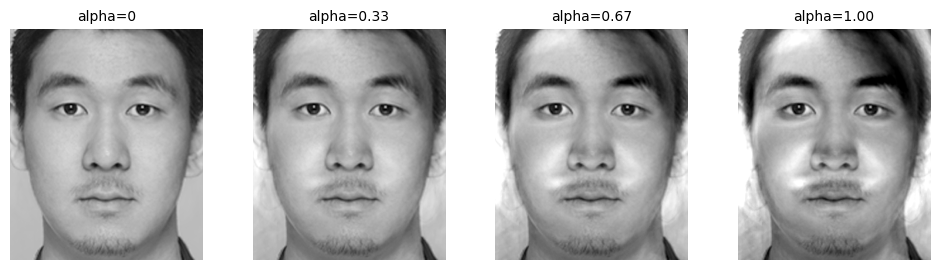
The results are given by:

The left-most and right-most images are the results of extrapolation, while other images are results of interpolation.

Part VI: Bells and Whistles - PCA Face

This part is given by:
1. Calculate a PCA basis on dataset
2. Visualize components
3. Create better caricature on PCA method
The PCA result on FEI_female1 is given as follows (we take the first 10 components):
Suppose we want to make my face more "feminine". We can implement that based on enhancing PCA Component weight.

The result is shown as follows: